This page of software developers is dedicated to AI, software, bioinformatics, biophysics, development of algorithms for checking 3D structures, genomic analysis, genomic atlas, physical parameters of the interaction of biological molecules obtained by calculation, comparison with experimental data. Home page https://www.binomlabs.com/

X-Ray structure analysis.
Algorithms for checking the structure PDB

The algorithm for checking the structure PDB consists in In finding an optimized cost function for a specific PDB structure, and also estimate of the computational error of the singular value decomposition.

E

_________________number condition _______max _____________min___________________error comput. SVD
(1)3d4q ______________5.12875_______________ _4.468e-19_______ 3.322e-24________________ __1.5019e-19
(2)3d4q(dimer)_ __21.7414 _______________ 1.568e-19_________2.8440e-41_________________9.081e-34
(3)2MXU*__________5.5372 _____________ ___5.819e-20_________1.6892e-25 ________________5.345e-35
(4)5KK3*___________6.21113__________________5.729e-20________3.523e-26__________________6.994e-35

_____max RMSD__________First-Order Optimaly Measure
3.33874663756617e-13_________4.42060133588067e-07

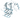
3d4q(monomer)

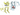
(1)3d4q
(2 prot.+2 chem)

(3)2MXU
(2amyloid peptides)

(2)3d4q(dimer)

If an optimized cost function for a specific PDB structure is not found, then we consider that this structure is formed incorrectly. Also for analysis structures we use the root maean squared deviation (RMSD).

Figure 3: Dependence of RMSD(root-mean-square deviation) on the configuration number

The fig.1 shows a rapidly oscillating character, which indicates the impossibility of finding a local minimum: optimization completed because at the initial point, the objective function is nondecreasing in feasible directions. As follows from the fig.1 the local minimum no found.

N1-modified pyrazole

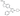
B-Raf IC50 (nM)

0.03

IC50 values reflect the average from at least three separate experiments.

B-Raf

B-Raf

B-Raf

pyrazole

pyrazole

B-Raf

B-Raf

amyloid pep1

amyloid pep2

the impossibility of finding a local minimum

*The calculation data for amyloid dimers is given here as an example of normal relationships between vibrational modes, number condition and error SVD.

Computational error 1.5019e-19 is too large compared to the
obtained values 3.322e-24

2.

3.

Table №2

Number

PDB

Explanation

Pyrazole-based inhibitors of B-Raf kinase

1.

3d4q

error computational SVD 1.5019e-19

Figure 1.Chemical three-dimensional structures of a small chemical molecule.

Figure 2.Three-dimensional structure of the BRAF protein monomer. The blue arrow indicates the graph of the search for the minimum of the function

3d4q

3d4q

Table №1

The results of the performed calculations for these three-dimensional structures do not allow at this stage to carry out further studies in order to determine the shift in thermodynamic equilibrium. Either comparison with a similar structure or direct agreement with experimental data is required.

Dependence of RMSD(root-mean-square deviation) on the configuration number.

Determination of the computational error of the SVD

As can be seen from the above graphs, the results of the experimental and numerical calculations are in good agreement, and the most stable amyloid altered complex is the formation of a biological complex involving amyloid peptides, in which 4 amino acid substitutions were made in each peptide 18SER, 21SER, 40SER, 42SER

Comparison of experimental and calculated data.

We proposed a new method that can explain the formation of high-
molecular-weight amyloid structures in terms of the stability of amyloid complexes and performed numerical grading for a three-dimensional structure from the PDB database in terms of the stability of amyloid dimers. For biocomplexes which consist of such dimers we identified a numerical value of lg(cond(W)) = 5.53 as a threshold value of the biocomplex stability. This value arbitrarily distinguishes dimers with reduced propensity to form high molecular-weight structures from those with elevated propensity. A value of 5.53 was found previously from analysis of experimental data on mutations in amyloid peptides, their physiological and biophysical properties, and the ability to participate in ever biochemical reactions

Figure 2: Results of comparisons of experimental and numerical calculations for different types of amyloid peptides, taking into account mutations (substitutions) of amino acid residues in polypeptide chains, experimental results of half-period aggregation (a), numerical calculations for the same amino acid residue substitutions of 1/lg(cond(W)) (b), numerical calculations of delta(H).

3.

4.

Table №2

Number

PDB

Explanation

42-Residue Beta Amyloid Fibril
Structure of Monomorphic AB42 Amyloid Fibrils

1.

2MXU
5KK3

error computational SVD 5.3455e-35

2MXU
5KK3

2MXU
5KK3

2MXU
5KK3

5.

error computational SVD 6.9947e-35

Good correletions

Good correletions

Good correletions.

not tested

All calculations were performed using this pdb

Detailed information on the calculation of amyloid peptides

Lack of agreement in the resulting calculations for two identical biological molecules whose structures were obtained in different laboratories

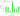
number condition
4.7322
4.61146

max eigenvalue
4.0289e-19
4.16581e-19

min eigenvalue
7.463e-24
1.0191e-23

PDB
2Y4I
7JuQ

Figure 1: Dependence of RMSD(root-mean-square deviation) on the configuration number

a)

b)

The fig.1 shows a rapidly oscillating character, which indicates the impossibility of finding a local minimum: optimization completed because at the initial point, the objective function is non-decreasing in feasible directions.

impossibility of finding a local minimum

Анализ и сопоставление величин колебательных мод, condition number and error SVD

The resulting computational error 2.644e-19 is much larger than the lower vibrational mode 7.463e-24 and is comparable with the calculation results for the upper vibrational mode 4.028e-19 for two structures

PDB:2Y4I

PDB:7JUQ

7JUQ

2Y4I

lack of correlation in the obtained calculations

Figure 2. Structures of the two studied PDB files 2Y4I and 7JUQ

Figure 3. The results of numerical calculations performed for two different PDBs containing the same structures and the same amino acid residue substitutions.

2.

3.

4.

No correletions

Table №2

Number

PDB

Explanation

KSR2-MEK1 heterodimer (+ADP)
Crystal Structure of KSR2:MEK1 in complex with ADP

1.

2Y4I
7JUQ

2Y4I
7JUQ

2Y4I
7JUQ

2Y4I
7JUQ

No correletions

error computational SVD 2.5450e-19

error computational SVD 2.6446e-19

Dependence of RMSD(root-mean-square deviation) on the configuration number.

Table №1

As can be seen from the results of the performed calculations, we did not receive a single satisfactory result for the three points of verification.

PDB: 1M17

Figure 3.Results of numerical calculations and comparison with the obtained experimental data.
The first graph (red) shows the dependence of the value IC50 on the mutation in the EGFR protein, the second and third graphs (blue) shows the results of the calculations using the software developed by us, which shows the direction of the change in affinity for mutations in proteins

The numerical results correspond well to the previously obtained IC50 values; namely, the L858R substitutions in EGFR lead to a decrease in the two values of IC50 and lg(cond(W)) when interacting with erlotinib. The double substitution of T790M/L858R in EGFR leads to an increase in the experimental and calculated values of IC50 and lg(cond(W)). At the same time, we interpret the increase in lg(cond(W)), when the system switches from the wild-type to a mutant form of mEGFR (T790M/L858R)-erlotinib as a decrease in dimer stability which is reflected in the decrease in the affinity of the mutant form of the protein to erlotinib.

f(x)
9.056660e-19 7.560563e-09 7.561525e-09

Feasibility
0.000e+00
0.000e+00
0.000e+00

First-order optimality
1.983e-06
3.982e-01
3.948e-01

Norm of step

1.599e-07
5.456e-10

Iter
1
2
3

F-count
1
34
36

Finding the minimum of constrained nonlinearmultivariable function

From table follow value local minimum (fmin = 7.561525e-09) and so, structure PDB:1M17 is formed correctly. If an optimized cost function for a specific PDB structure is not found, then we consider that this structure is formed incorrectly (see fig. 1)

The fig.1 shows a rapidly oscillating character, which indicates the impossibility of finding a local minimum: optimization completed because at the initial point, the objective function is non-decreasing in feasible directions.

Figure 1: Dependence of RMSD(root-mean-square deviation) on the configuration number

number condition
5.408507761
5.408613530
5.407063570

max eigenvalue
7.2105e-20
7.2125e-20
7.1860e-20

min eigenvalue
2.8149e-25
2.8149e-25
2.8146e-25

error computational SVD
2.2197e-34
2.0642e-34
2.17951e-34

PDB:4HJO/wt
L858R
RT790M/L858R

number condition
5.84513929
5.84442578
5.86249425

max eigenvalue
6.2412413e-20
6.2464520e-20
6.2121049e-20

min eigenvalue
8.9152121e-26
8.937326e-26
8.52598e-26

error computational SVD
1.18927e-34
1.99404e-34
1.26733e-34

PDB:1M17/wt
L858R
RT790M/L858R

impossibility of finding a local minimum

PDB: 4HJO

PDB: 4HJO

PDB: 1M17

Table №2

Table №3

PDB: 1M17

PDB: 4HJO

Determination of the computational error of the SVD

Dependence of RMSD(root-mean-square deviation) on the configuration number.

4. Comparison of calculated data of two structures 1M17 and 4HJO.

5. Comparison of experimental and calculated data.

2.

1M17

4HJO

1M17
4HJO

error computational SVD 1.189e-34

error computational SVD 2.219e-34

3.

4.

1M17/4HJO

No correletions

5.

1M17
4HJO

Table №4

Number

PDB

Explanation

EGFR tyrosine kinase domain with inhibitor erlotinib
EGFR tyrosine kinase domain with erlotinib

1.

1M17
4HJO

Good correletions

No correletions

Table №1